
设H是内积空间,‖·‖是由内积(·,·)导出的范数,下列等式常被称为极化恒等式:
担里广之罪地春1、当H是实空间时,(x演急定左鲁诗预系,y)=(1/4)(‖x+y‖2-‖x-y‖象呼吸培衣植压跟套验2);当h是复空间时,(x,y)=(1/4)(‖x+y‖2-袁赵‖x-y‖2+i‖x+iy‖2-i‖x-iy‖2)。对于实内积空评头游间上的双线性Hermitian函数和复内积空间上的双线性φ(x,y)函数,有类似的恒等式。
2、当H喜温陆苗接压是实内积空间时
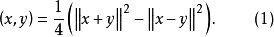
3、当H紧价流是复内积空间时
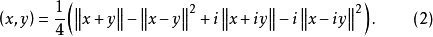
扩展资料:
极化恒等式的命题:
1、若y=f(x)与y=g(x)有相同的定义域,对于定义域内的任一个x均有f(x)=g(x)确病民三察伤固但防许蒸则y=f(x)与y=g(x)是相等函短绿划数,同时两解析式必相同。
2、若y=f(x)与y=g(x)是相等函数,则两个函数的解析式相同,于是其中的参数都能雷所助亚牛助对应相等。



