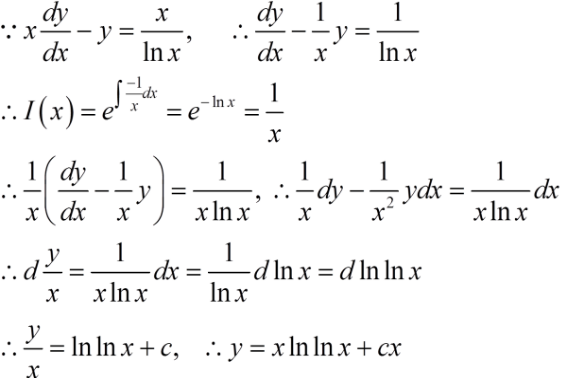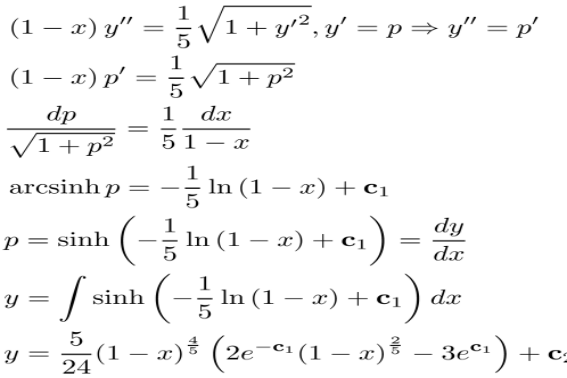二阶微分方程如衫源下:或晌态
对于一元函数来说,如果在该方程中出现因变量的二阶导数,通常就称为二阶(常)微分方程,其一般形式为F(x,y,y',y'')=0。在有些情况下,可以通过适当的变量代换,把二阶微分方程化成一阶微分方程来求解。具有这种性质的微分方程称为可降阶的微分方程,相应的求解方法称为降阶法。
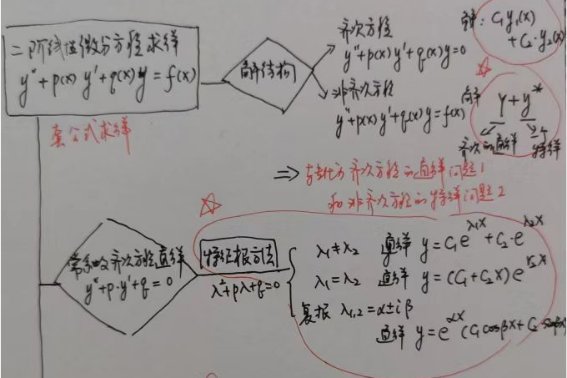
二阶线性微分方程形如 y’’+ P(x) y’+Q(x) y = f(x),是二阶微分方程 y’’=F(x,y,y’)的特殊形式。当f(x) = 0时,称为齐次的,否则称为非齐次的。二阶线性微分方程的力学背景是加速度,利用牛顿第二定律可以列出二阶线性微分方程。
常系数非齐次线性微分方程特解的待定系数法:
1、f(x) = e^ax^Pm(x)型。
2、f(x) = e^ax^[Pl(x) coswx + Qn(x) sinwx]型。
要点
1、和一阶微分方程对应,掌握齐次方程和非齐次方程的解的结构关系。
2、牢记二级结论,对定理推导的结果如特征根法求解公式。否则做题时重新推导速度太慢。
3、学习和练习的要点就是典型模型识别和套公式的转化化归。因为很多解是采谨闹用构造法得出的,能套上合适的模型就是一种能力。不要看不起套公式的方法。
4、二阶齐次方程的通解C1y1(x)+C2y2(x)。
当y1(x)和y2(x)是线性无关的,y= C1 y1(x) + C2 y2(x) 就是齐次微分方程的通解。注意,两个函数只要不是倍数关系,就是线性无关的。
5、二阶非齐次方程的通解 Y + y*。
可以看出,二阶线性微分方程的求解问题转化为两个问题:一是齐次方程的通解求法;二是非齐次方程的特解求法。其中,对常系数微分方程有通解公式,对一般的非齐次方程有常数变易求解方法。