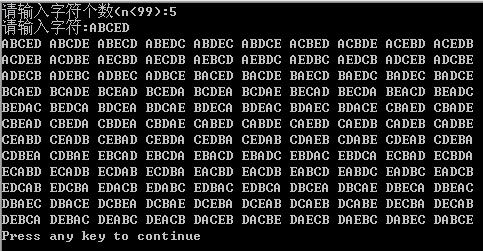
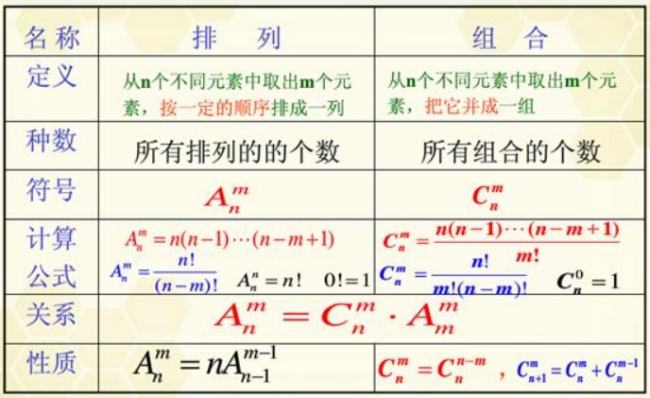
全排列数f(n)=n!(定义0!=1) 1,2,3
1,3,2
2,1,3
2,3,1
3,2,1
3,1,2
这是由于算法只是考虑到了如何输出全排列,而没有考虑到换位是否有问题。
所以我提出了解决方案,就是换位函数修改下
如 1 2 3 换位的话 ,不应该直接 3 2 1这样 ,
让3和1直接换位; 而是让3排在最前后 ,1 2 依次向后 以下介绍全排列算法四种:
(A)字典序法
(B)递增进位制数法
(C)递减进位制数法
(D)邻位对换法 对给定的字符集中的字符规定了一个先后关系,在此基础上规定两个全排列的先后是从左到右逐个比配陵族较对应的字符的先后。
[例]字符集{1,2,3},较小的数字较先,
这样按字典序生成的全培弊排列是:123,132,213,231,312,321。
[注意] 一个全排列可看做一个字符串,字符串可有前缀、后缀。
1)生成给定全排列的下一个排列 所谓一个的下一个就是这一个与下一个之间没有其他的。这就要求这一个与下一个有尽可能长的共同前缀,也即变化限制在尽可能短的后缀上。
[例]839647521是1--9的排列。
1—9的排列最前面的是123456789,最后面的是987654321,从右向左扫描若都是增的,就到987654321,也就没有下一个了。否则找出第一次出现下降的位置。 1)由排列求中介数 在字典序法中,中介数的各位是由排列数的位决定的.中介数位的下标与排列的位的下标一致。
在递增进位制数法中,中介数的各位是由排列中的数字决定的。即中介数中各位的下标与排列中的数字(2—n)一致。可看出n-1位的进位链。 右端位逢2进1,右起第2位逢3进1,…,
右起第i位逢i+1进1,i=1,2,…,n-1. 这样的中介数我们称为递增进位制数。 上面是由中介数求排列。
由序号(十进制数)求中介数(递增进位制数)如下:
m=m1,0≤m≤n!-1
m1=2m2+kn-1,0≤kn-1≤1
m2=3m3+kn-2,0≤kn-2≤2
……………
mn-2=(n-1)mn-1+k2,0≤k2≤n-2
mn-1=k1,0≤k1≤n-1
p1p2…pn←→(k1k2…kn-1)↑←→m
在字典序法中由中介数求排列比较麻烦,我们可以通过另外定义递增进位制数加以改进。
为方便起见,令ai+1=kn-1,i=1,2,…,n-1
(k1k2…kn-1)↑=(anan-1…a2)↑
ai:i的右边比i小的数字的个数
在这样的定义下,
有839647521←→(67342221)↑
(67342221)↑+1=(67342300)↑←→849617523
6×8+7)×7+3)×6+4)×5+2)×4+2)×3+2)×2+1 =279905
由(anan-1…a2)↑求p1p2…pn。
从大到小求出n,n-1,…,2,1的位置
_ ... _ n _ _ …_ (an个空格)
n的右边有an个空格。
n-1的右边有an-1个空格。
…………
2的右边有a2个空格。
最后一个空格就是1的位置。 在递增进位制数法中,中介数的最低位是逢2进1,进位频繁,这是一个缺点。
把递增进位制数翻转,就得到递减进位制数。 (anan-1…a2)↑→(a2a3…an-1an)↓
839647521→ (12224376)↓
(12224376)↓=1×3+2)×4+2)×5+2)×6+4)×7+3)×8+7)×9+6=340989
[注意]求下一个排列十分容易 递减进位制数法的中介数进位不频繁,求下一个排列在不进位的情况下很容易。
这就启发我们,能不能设计一种算法,下一个排列总是上一个排列某相邻两位对换得到的。
递减进位制数字的换位是单向的,从右向左,而邻位对换法的换位是双向的。 这个算法可描述如下:
对1—n-1的每一个偶排列,n从右到左插入n个空档(包括两端),生成1—n的n个排列。
对1—n-1的每一汪核个奇排列,n从左到右插入n个空档,生成1—n的n个排列。
对[2,n]的每个数字都是如此。
839647521
字典序法 递增进位制法 递减进位制法 邻位对换法
下一个 839651247 849617523 893647521 836947521
中介数 72642321↑ 67342221↑ 12224376↓ 10121372↓
序 号 297191 279905 340989 203393