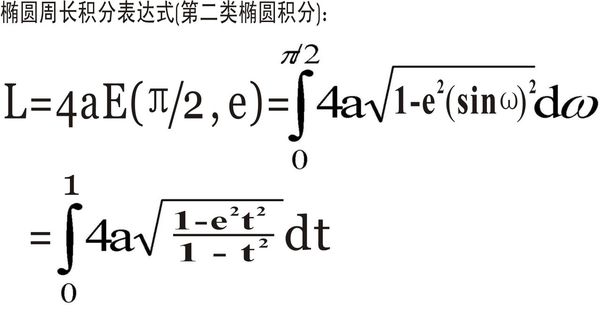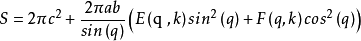椭圆周长公式:L=2πb+4(a-b)
椭圆周长定理:椭圆的周长等于该椭圆短半轴长为半径的圆周长(2πb)加上四倍的该椭圆长半轴长(a)与短半轴长(b)的差。
扩展资料:
最早由阿贝尔提出,欧拉发展。
对这类问题的讨论引出一门数学分支--椭圆积分(变分法),仍然方兴未艾。
以下是几个比较简单的近似公式:
公式一至公式六为一般精度,满足简单计算需要;
公式八为高精度,满足比较专业一些的计算需要。
椭圆周长公式:L=2πb+4(a-b)
这些公式均符合椭圆的基本规律,当a=b时,L=2aπ,
1、 L1 =π·qn/ atan(n)
(b→a,q=a+b,n=((a-b)/a))^2
这是根据圆周长和割圆术原理推导雹肆的,精度一般。
2、 L2 =π·θ/(π/4)·(a-c+c/sinθ)
(b→0,c=√(a^2-b^2),θ=acos((a-b)/a)^1.1)
这是根据两对扇形组成椭滚局圆得特点推导的,精度一般。
3、 L3 =π·q(1 +mn)
(q=a+b,m=4/π-1,n=((a-b)/a)^3.3)
这是根据圆周长公式推导的,精度一般。
4、 L4 =π·√(2a^2 + 2b^2)·(1 +mn)
(m=2√(2/π)-1,n=((a-b)/a)^2.05)
这是根据椭圆a=b时得基本特点推导的,精度一般。
5、 L5 = √(4ab·π^2 + 15(a-b)^2)·(1 +mn)
(m=4/√(15)-1 ,n=((a-b)/a)^9 )
这是根据椭圆a=b,c=0时是特点推导的,精度较好。
6、L6= π√[2(a^2+b^2)] (较近似)
7、L7=π[3/2(a+b)-√(ab)] (较精确)
8、L8 =π·q(1 + 3h/(10 + √(4-3h)))·(1 +mn)
(q=a+b,h=((a-b)/(a+b))^2,m=22/7π-1,n=((a-b)/a)^33.697)
这是根源备轿据椭圆标准公式提炼的,精度很高。