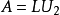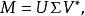Simone这是用cramer法则求解方程组。
注意一个特征：系数矩阵所有列的元素和都一样，因此，可以把前n-1行都加到第n行，此操作不改变行列式的值，（注意讨论a的取值，对后续操作有影响），然后再利用第n行把第i行上的数字i变为0，其中i=1,2,3,n-1，
注意：此操作改变行列式的值，这些操作结束之后，系数矩阵就变成只有对角线元素和最下边一行元素非0的对角阵。
第一个矩阵的第一行 的每个数分别乘以 第二个矩阵第一列 的每个数 相加求和是结果矩阵的 第一个数；
第一个矩阵的第二行 和 第二个矩阵的第一列 求和 是结果矩阵的第一列第二个数；
以此类推。
两个矩阵要做乘法，那么第一个矩阵的行数和第二个矩阵的列数必须一样，就是m✖️n的矩阵，和n✖️s的矩阵，可以做乘法。
扩展资料：
矩阵分解是将一个矩阵分解为比较简单的或具唤告有某种特性的若干矩阵的和或乘积 [14] ，矩阵的分解法一般有三角分解、谱分解、乎手奇异值分解、满秩分解等。
三角分解
设
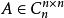,则A可以唯一地分解为A=U1R ,其中U1是酉矩阵，R是正线上三角复矩阵，或A可以唯一地分解为其中L是正线上三角复矩阵，是酉矩阵
谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需岁链嫌要注意只有对可对角化矩阵才可以施以特征分解 [17] 。
奇异值分解
假设M是一个m×n阶矩阵，其中的元素全部属于域K，也就是实数域或复数域。如此则存在一个分解使得
其中U是m×m阶酉矩阵；Σ是m×n阶实数对角矩阵；而V*，即V的共轭转置，是n×n阶酉矩阵。这样的分解就称作M的奇异值分解 [18] 。Σ对角线上的元素Σi,i即为M的奇异值。常见的做法是将奇异值由大而小排列。如此Σ便能由M唯一确定了。
参考资料来源：百度百科-矩阵
