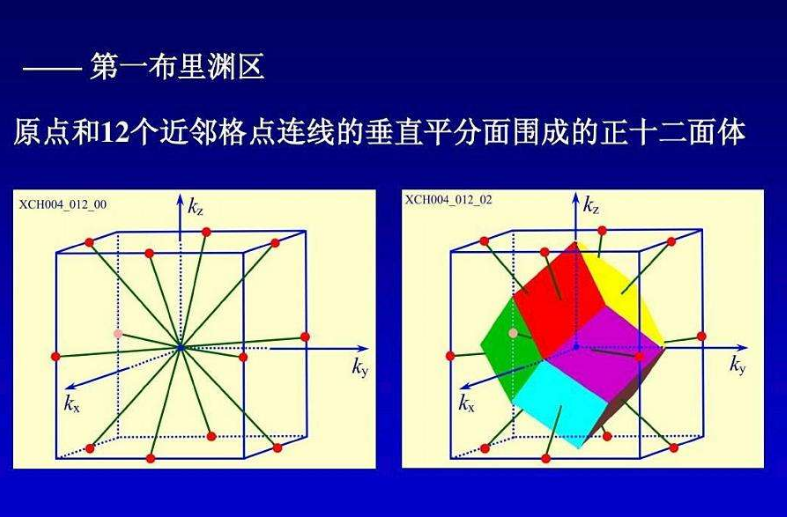
布里渊区(Brillouin zone) ,在数学和固体物理学中,第一布里渊区是动量空间中晶体倒易点阵的魏格纳-塞兹原胞(Wigner-Seitz cell)。
固体的能带理论中,各种电子态按照它们的波矢分类。在波矢空间中取某一倒易阵点为原点,作所有倒易点阵矢量的垂直平分面,这些面波矢空间划分为一系列的区域:其中最靠近原点的一组面所围的闭合区称为第一布里渊区。
在第一布里渊区之外,由另一组平面所包围的波矢区叫第二布里渊区;依次类推可得第三、四、…等布里渊区。
扩展资料:
布里渊区的特点
布里渊区的形状取决于晶体所属布喇菲点阵的类型。简单立方、体心立方和面心立方点阵的简约区分别为立方体,菱十二面体和截角八面体(十四面体)。
它们都谈州是对称的多面伍没体,并具有相应点阵的点群对称性,这一特征使简约区中高对称点的能量求解得以简化(见晶体的对称性)。
由于晶体中的格波或者电子波的色散关系在波矢空间是周期为π/a的周期性函数(例如,E(k) = E(k+π/a),则k和k+π/a表腔侍纳示相同的状态。
因此可把波矢限制在第一Brillouin区(-π/a < q < π/a ) 内,而将其他区域通过移动n/a而合并到第一Brilouin区;在考虑能带结构时, 只需要讨论第一Brilouin区就够了。
参考资料来源:百度百科-布里渊区