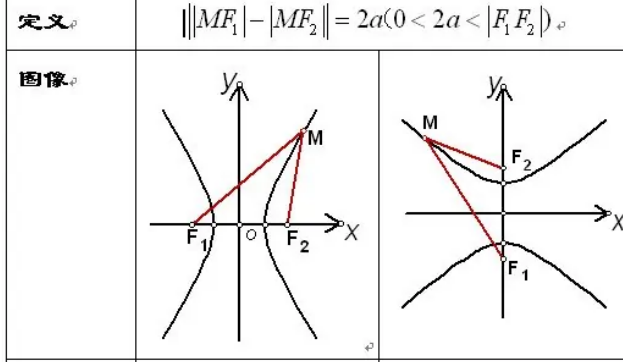
双曲线的标准方程如下:
标准方程1:焦点在X轴上时为x2/a2-y2/b2=1(a>0,b>0)。
标准方程1:焦点在Y轴世团镇上时为y2/a2-x2/b2=1(a>0,b>0)。
双曲线取值范围:│x│≥a(焦点在x轴上)或者│y│≥a(焦点在y轴搜粗上)。
双曲线对称性:关于坐标轴和原点对称,其中关于原点成中心对称。
双曲线的定义:
(1)平面内,到两个定点的距离之差的绝对值为常数(小于这两个定点间的距离)的点的轨迹称为双曲线。定点叫双曲线的焦点。
(2)平面内,到给定一点及一直或举线的距离之比为常数e(e=c/a(e>1),即为双曲线的离心率)的点的轨迹称为双曲线。定点叫双曲线的焦点,定直线叫双曲线的准线。双曲线准线的方程为x=±a²/c(焦点在x轴上)或y=±a²/c(焦点在y轴上)。
(3)一平面截一圆锥面,当截面与圆锥面的母线不平行,且与圆锥面的两个圆锥都相交时,交线称为双曲线。
以上内容参考:百度百科-双曲线的标准方程